Talmängder
Är du nyfiken att lära dig följande mängder det vill säga de klassiska talmängder: naturliga tal, heltal,rationella och irrationella samt reella tal Läs vidare.
För att underlätta förståelse om talsystem har man organiserat det i olika så kallade Talmängder. Här de vanligaste/klassiska talmängder; naturliga tal (N), heltal (Z), rationella tal (Q), irrationella tal och reella tal (R) .
Mängden av naturliga talen betecknas med bokstaven N. Notera att i visa skrifter säges att nollan tillhör till det naturliga talmängden (0 ∈ Ν) och den illustreras enligt följande; N = {0, 1, 2, 3, …, }.
Däremot i visa skrifter säges att nollan inte tillhör till mängden av naturliga tal (0 ∉ Ν) och den illustreras enligt följande; gör det. N = {1, 2, 3, …, }. Den här varianten kan också kallas ibland för mängden av positiva heltal. I material som publiceras här om inget annat anges, N kommer representera mängden av naturliga tal utan nollan. Med andra ord N = {1, 2, 3, …, }.
Notera att ( … ) indikerar att mönstret försätter.
Mängden av heltal betecknas med bokstaven Z. Här ingår alla positiva och negativa heltal. Mängden av naturliga tal ingår i mängden av heltal. Mängden av heltal kan illustreras enligt följande;
Z = {…, -3, 2, 1, 0, 1, 2, 3, …, }.
Rationella är tal som kan skrivas på formen a / b, a och b tillhör mängden av heltal (a, b ∈ Z) samt b är skild från noll (b ≠ 0). Mängden av rationella tal kan illustreras enligt följande;
Q = { a / b : a, b ∈ Z och b ≠ 0}.
Bra och veta
- Ett heltal a är ett rationellt tal, eftersom den kan skrivas på formen a / 1.
- Alla heltal tillhör rationella tal, men alla rationella tal inte tillhör heltal.
- Ett tal med ändlig eller oändligt men som har periodisk decimal utveckling är rationella tal.
Notera:
- Med ’periodisk decimal utveckling’ menas att det går och hitta ett mönster i decimalernas följd. Till exempel x = 6.357 432 432 432 432 …, här 432 upprepas i all oändlighet. Här x är ett rationellt tal.
- Med ’ändlig’ menas att det finns det sista decimal. Till exempel a = 7.8523. Här vi har ett rationellt tal med ändligt decimal utveckling.
- Med ’oändlig’ menas här, att det inte finns ett sista decimalt tal. Talet x ovan är ett exempel på ett rationellt tal med oändligt samt periodiskt decimal utveckling.
Tal som har oändligt decimal utveckling samt inte är periodisk decimal utveckling är irrationella tal. Några exempel på irrationella tal är:√2 och π .
Notera:
- Med ’inte är periodisk’ menas att det inte går att hitta ett mönster i decimalernas följd.
De rationella och irrationella talmängder tillsammans bilder det talmängd som kallas för reella tal. Mängden av reella tal betecknas med R.
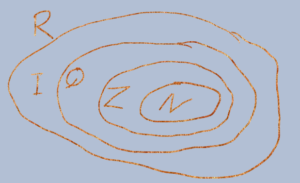
Eftersom naturliga tal tillhör mängden av heltal, mängden heltal i tillhör mängden av rationella tal och i slutänden rationella tal och irrationella tillsammans bildar mängden av reella tal. Kan man samman fatta det hela enligt figuren nedan.
Relaterade Video
Nedan kan du se videon som täcker ovan nämnda områdena:
Inget relaterade video i dagsläge